Cette expérience montre comment, grâce à la force centrifuge, une petite masse peut facilement en entraîner une plus grosse. Elle illustre également la conservation du moment cinétique de rotation.
Fiche d’accompagnement de l’expérience:
Matériel-
une masse d’environ 100 g ;
-
une masse d’environ 20 g dans un matériau aussi mou que possible, par exemple un bouchon en caoutchouc ou un boulon;
-
un morceau de tube (longueur : environ 15 cm) de diamètre assez faible, à la rigueur une paille ou un corps de stylo bille;
-
du fil (longueur : environ 1 m).
Montage et réalisationPrendre un tube creux de faible diamètre, par exemple le corps d’un crayon à bille.
Passer un fil solide dans le tube et y accrocher d’un côté une masse d’environ 100 grammes et de l’autre une masse beaucoup plus petite, un écrou de quelques grammes par exemple. L’ensemble doit pouvoir coulisser librement à travers le tube et la différence des deux masses doit se voir nettement.
Tenir le tube verticalement dans une main, la petite masse placée sur son extrémité supérieure, tirer sur le fil et mettre la petite masse en rotation. (Il faut éventuellement soulever un peu la masse la plus grande au départ pour permettre la mise en rotation de la petite masse).
Celle-ci ne tarde pas à tirer sur le fil et à faire remonter la grosse masse.
C’est la force centrifuge développée par la rotation de la petite masse qui, en dépit de son faible poids, est suffisante pour soulever une masse beaucoup plus importante.
ExplicationsLa masse accrochée au fil permet d’exercer sur la masse tournante la force centripète nécessaire à son mouvement de rotation.
La valeur de la force centripète dépend du rayon du cercle décrit (donc de la longueur de fil disponible) et de la vitesse angulaire (qui résulte du mouvement de la main qui tient le tube). Les forces s’exerçant sur le système dépendent donc du mouvement de la main qui tient le tube.
Pour montrer la conservation du moment cinétique on diminue le moment d’inertie du système en réduisant la longueur du fil qui tourne.
Cette opération ne modifie pas le moment cinétique du système car la force exercée sur la ficelle a un moment nul.
La diminution du moment d’inertie I provoque une augmentation de la vitesse angulaire ω car la valeur du moment cinétique L = I.ω reste constante.
Si L reste constant, l’énergie cinétique de rotation augmente car
.
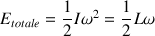L’augmentation d’énergie cinétique résulte du travail fourni par l’opérateur pour tirer la deuxième masse vers le bas.
La formule précédente montre qu’on ne peut pas avoir simultanément conservation du moment cinétique et conservation de l’énergie cinétique.
RemarquesIl est préférable que le matériau constituant la petite masse soit aussi mou que possible pour éviter toute blessure au cas où la masse percuterait quelqu’un en tournant ou bien au cas où le fil se casserait.